Training a transfer learning model

Training a transfer learning model#

This tutorial illustrates how to use a transfer learning approach to train a model on the GC mEPSP dataset. The miniML base model, trained on GC mEPSCs, is used as a starting point. We freeze the convolutional layers of the base model and train the remaining layers on the GC mEPSP dataset. This transfer learning approach greatly reduces the training time and the required size of the training dataset.

Preparation#

We begin by downloading the training dataset for training a miniML mEPSP detection model from Zenodo. The dataset contains labeled data segments of mEPSPs and non-events.

import requests

file_url = 'https://zenodo.org/records/14507343/files/2_GC_mepsp_train.h5'

response = requests.get(file_url)

if response.status_code == 200:
    with open('../_data/GC_mEPSP_training_data.h5', 'wb') as file:
        file.write(response.content)
    print('Downloaded GC_mEPSP_training_data.h5')

Downloaded GC_mEPSP_training_data.h5

Now we set up our Python environment:

import tensorflow as tf
from sklearn.preprocessing import minmax_scale
from sklearn.model_selection import train_test_split
from sklearn.metrics import auc, confusion_matrix, ConfusionMatrixDisplay, roc_curve
from tensorflow.keras.layers import (Input, BatchNormalization, AveragePooling1D, Conv1D, 
                                     Bidirectional, LSTM, Dense, Dropout, LeakyReLU)
from tensorflow.keras.optimizers.legacy import Adam
from scipy.signal import resample
import h5py
import numpy as np
import time
import matplotlib.pyplot as plt
import warnings

print('Using TF version', tf.__version__)
print('GPUs available:', len(tf.config.list_physical_devices('GPU')))

Using TF version 2.15.0
GPUs available: 1

Set training parameters#

We set the training parameters in a dictionary called settings.

settings = {
    'training_size': 0.8,
    'testing_size': None,
    'learn_rate': 2e-8,
    'epsilon': 1e-8,
    'patience': 12,
    'epochs': 100,
    'batch_size': 64,
    'dropout': 0.5,
    'training_data': '../_data/GC_mEPSP_training_data.h5',
    'base_model': '../../models/GC_lstm_model.h5'
}

Prepare training data#

Now we can start by loading the training dataset. The data is stored in a HDF5 file.

The data is loaded into the x and y variables. The data is resampled to 600 datapoints and the events are inverted. Because the base model was trained to detect downward deflections, inverting the data helps when training on data having a different direction. When using the trained model, remember to set the event_direction parameter to ‘positive’ when generating the EventDetection object.

with h5py.File(f'{settings["training_data"]}', 'r') as f:
    x = f['events'][:]
    y = f['scores'][:]

fig, axs = plt.subplots(1, 2, figsize=(8,3.5))
axs[0].plot(x[505], c='#425066')
axs[0].set_title('before resampling and inverting\n')

# resample and invert the data
x = resample(x, 600, axis=1)
x *= -1

axs[1].plot(x[505], c='#425066')
axs[1].set_title('after resampling and inverting\n')
plt.tight_layout()
plt.show()

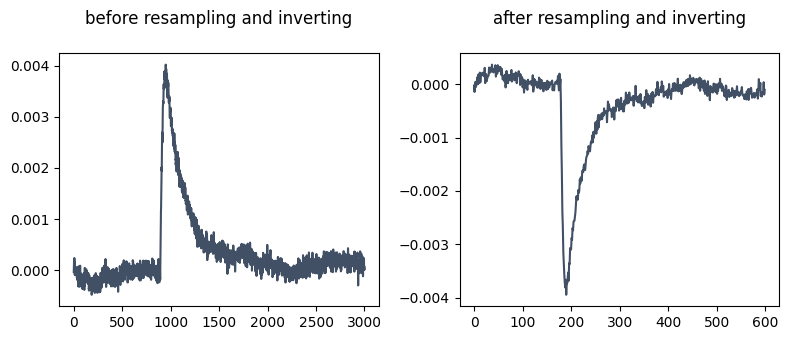
../_images/06b655cc0d3d2d5cc44e6d6fdeae14d0eff35f2dded2c9297db3d19bb0a0a0ec.png

Next, we proceed as for full model training by min-max scaling and splitting the data into training and testing sets.

scaled_data = minmax_scale(x, feature_range=(0,1), axis=1)
scaled_data = np.expand_dims(scaled_data, axis=2)
merged_y = np.expand_dims(y, axis=1)

print(f'loaded events with shape {scaled_data.shape}')
print(f'loaded scores with shape {merged_y.shape}') 
print(f'ratio of pos/neg scores: {merged_y.sum()/(merged_y.shape[0]-merged_y.sum()):.2f}')

if merged_y.sum()/(merged_y.shape[0]-merged_y.sum()) > 1.05:
    warnings.warn("unbalanced dataset: ratio of positive and negative scores >1.05")
elif merged_y.sum()/(merged_y.shape[0]-merged_y.sum()) < 0.95:
    warnings.warn("unbalanced dataset: ratio of positive and negative scores < 0.95")

x_train, x_test, y_train, y_test = train_test_split(scaled_data, merged_y, train_size=settings['training_size'], random_state=1234)

loaded events with shape (4004, 600, 1)
loaded scores with shape (4004, 1)
ratio of pos/neg scores: 1.01

Prepare the model#

def build_model(x_train, dropout_rate):
    model = tf.keras.models.Sequential()
    model.add(Input(shape=(x_train.shape[1:])))
              
    model.add(Conv1D(filters=32, kernel_size=9, padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU())
    model.add(AveragePooling1D(pool_size=3, strides=3))
    
    model.add(Conv1D(filters=48, kernel_size=7, padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU())
    model.add(AveragePooling1D(pool_size=2, strides=2))
    
    model.add(Conv1D(filters=64, kernel_size=5, padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU())
    model.add(AveragePooling1D(pool_size=2, strides=2))
    
    model.add(Conv1D(filters=80, kernel_size=3, padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU())
    
    model.add(Bidirectional(LSTM(96, dropout=dropout_rate), merge_mode='sum'))
    model.add(Dense(128, activation=LeakyReLU()))
    model.add(Dropout(dropout_rate))
    model.add(Dense(1, activation='sigmoid'))
    
    return model

Next, we save the model weights from the pre-trained miniML model (the GC mEPSC base model). We then create a new model instance and load the saved weights.

old_model = tf.keras.models.load_model(settings['base_model'], compile=True)
old_model.save_weights('../_data/gc_weights')

new_model = build_model(x_train, settings['dropout'])
new_model.load_weights('../_data/gc_weights')

2025-03-21 17:31:19.177930: I metal_plugin/src/device/metal_device.cc:1154] Metal device set to: Apple M1 Pro
2025-03-21 17:31:19.177955: I metal_plugin/src/device/metal_device.cc:296] systemMemory: 16.00 GB
2025-03-21 17:31:19.177961: I metal_plugin/src/device/metal_device.cc:313] maxCacheSize: 5.33 GB
2025-03-21 17:31:19.177991: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:306] Could not identify NUMA node of platform GPU ID 0, defaulting to 0. Your kernel may not have been built with NUMA support.
2025-03-21 17:31:19.178003: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:272] Created TensorFlow device (/job:localhost/replica:0/task:0/device:GPU:0 with 0 MB memory) -> physical PluggableDevice (device: 0, name: METAL, pci bus id: <undefined>)

<tensorflow.python.checkpoint.checkpoint.CheckpointLoadStatus at 0x34cd23670>

For transfer learning, we have to freeze the convolutional layers of our model to prevent them from being trained. Only the remaining layers remain trainable.

for ind, layer in enumerate(new_model.layers):
    if layer.name == 'BatchNormalization':
        new_model.layers[ind].trainable = False
    else:
        if ind < len(new_model.layers) - 4:
            new_model.layers[ind].trainable = False
        else:
            new_model.layers[ind].trainable = True
              
new_model.compile(optimizer=Adam(learning_rate=settings['learn_rate'], epsilon=settings['epsilon'], amsgrad=True),
                  loss=tf.keras.losses.BinaryCrossentropy(),
                  metrics=['Accuracy'])

new_model.summary(show_trainable=True)

Model: "sequential"

____________________________________________________________________________

 Layer (type)                Output Shape              Param #   Trainable

============================================================================

 conv1d (Conv1D)             (None, 600, 32)           320       N

 batch_normalization (Batch  (None, 600, 32)           128       N

 Normalization)

 leaky_re_lu (LeakyReLU)     (None, 600, 32)           0         N

 average_pooling1d (Average  (None, 200, 32)           0         N

 Pooling1D)

 conv1d_1 (Conv1D)           (None, 200, 48)           10800     N

 batch_normalization_1 (Bat  (None, 200, 48)           192       N

 chNormalization)

 leaky_re_lu_1 (LeakyReLU)   (None, 200, 48)           0         N

 average_pooling1d_1 (Avera  (None, 100, 48)           0         N

 gePooling1D)

 conv1d_2 (Conv1D)           (None, 100, 64)           15424     N

 batch_normalization_2 (Bat  (None, 100, 64)           256       N

 chNormalization)

 leaky_re_lu_2 (LeakyReLU)   (None, 100, 64)           0         N

 average_pooling1d_2 (Avera  (None, 50, 64)            0         N

 gePooling1D)

 conv1d_3 (Conv1D)           (None, 50, 80)            15440     N

 batch_normalization_3 (Bat  (None, 50, 80)            320       N

 chNormalization)

 leaky_re_lu_3 (LeakyReLU)   (None, 50, 80)            0         N

 bidirectional (Bidirection  (None, 96)                135936    Y

al)

 dense (Dense)               (None, 128)               12416     Y

 dropout (Dropout)           (None, 128)               0         Y

 dense_1 (Dense)             (None, 1)                 129       Y

============================================================================

Total params: 191361 (747.50 KB)

Trainable params: 148481 (580.00 KB)

Non-trainable params: 42880 (167.50 KB)

____________________________________________________________________________

Training#

Now we can train our model using the mEPSP dataset. Only the previously selected layers are trained. Because we have initialized the model weights from the GC mEPSC base model, the training is also faster than for full model training.

early_stopping_callback = tf.keras.callbacks.EarlyStopping(
    monitor='val_loss',
    patience=settings['patience'],
    restore_best_weights=True)

start = time.time()

history = new_model.fit(x_train, y_train,
            verbose=2,
            epochs=settings['epochs'],
            batch_size=settings['batch_size'],
            validation_data=(x_test, y_test),
            shuffle=True,
            callbacks=[early_stopping_callback])

print('')
print('----')
print(f'train shape: {x_train.shape}')
print(f'score on val: {new_model.evaluate(x_test, y_test, verbose=0)[1]}')
print(f'score on train: {new_model.evaluate(x_train, y_train, verbose=0)[1]}')
print('----')
print(f'training time (s): {time.time()-start:.4f}')

Epoch 1/100

2025-03-21 17:31:21.050725: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:117] Plugin optimizer for device_type GPU is enabled.

51/51 - 4s - loss: 0.1969 - Accuracy: 0.9238 - val_loss: 0.2696 - val_Accuracy: 0.9238 - 4s/epoch - 87ms/step

Epoch 2/100

51/51 - 1s - loss: 0.1658 - Accuracy: 0.9341 - val_loss: 0.2314 - val_Accuracy: 0.9326 - 1s/epoch - 25ms/step

Epoch 3/100

51/51 - 1s - loss: 0.1560 - Accuracy: 0.9360 - val_loss: 0.2118 - val_Accuracy: 0.9351 - 1s/epoch - 25ms/step

Epoch 4/100

51/51 - 1s - loss: 0.1491 - Accuracy: 0.9404 - val_loss: 0.2232 - val_Accuracy: 0.9326 - 1s/epoch - 25ms/step

Epoch 5/100

51/51 - 1s - loss: 0.1416 - Accuracy: 0.9404 - val_loss: 0.2089 - val_Accuracy: 0.9351 - 1s/epoch - 26ms/step

Epoch 6/100

51/51 - 1s - loss: 0.1444 - Accuracy: 0.9410 - val_loss: 0.1903 - val_Accuracy: 0.9338 - 1s/epoch - 26ms/step

Epoch 7/100

51/51 - 1s - loss: 0.1328 - Accuracy: 0.9429 - val_loss: 0.1786 - val_Accuracy: 0.9338 - 1s/epoch - 26ms/step

Epoch 8/100

51/51 - 1s - loss: 0.1327 - Accuracy: 0.9482 - val_loss: 0.1753 - val_Accuracy: 0.9351 - 1s/epoch - 25ms/step

Epoch 9/100

51/51 - 1s - loss: 0.1253 - Accuracy: 0.9472 - val_loss: 0.1587 - val_Accuracy: 0.9326 - 1s/epoch - 26ms/step

Epoch 10/100

51/51 - 1s - loss: 0.1215 - Accuracy: 0.9500 - val_loss: 0.1751 - val_Accuracy: 0.9338 - 1s/epoch - 26ms/step

Epoch 11/100

51/51 - 1s - loss: 0.1211 - Accuracy: 0.9507 - val_loss: 0.1671 - val_Accuracy: 0.9338 - 1s/epoch - 26ms/step

Epoch 12/100

51/51 - 1s - loss: 0.1166 - Accuracy: 0.9479 - val_loss: 0.1458 - val_Accuracy: 0.9388 - 1s/epoch - 26ms/step

Epoch 13/100

51/51 - 1s - loss: 0.1212 - Accuracy: 0.9510 - val_loss: 0.1487 - val_Accuracy: 0.9388 - 1s/epoch - 26ms/step

Epoch 14/100

51/51 - 1s - loss: 0.1222 - Accuracy: 0.9491 - val_loss: 0.1470 - val_Accuracy: 0.9413 - 1s/epoch - 26ms/step

Epoch 15/100

51/51 - 1s - loss: 0.1219 - Accuracy: 0.9472 - val_loss: 0.1427 - val_Accuracy: 0.9413 - 1s/epoch - 26ms/step

Epoch 16/100

51/51 - 1s - loss: 0.1167 - Accuracy: 0.9504 - val_loss: 0.1485 - val_Accuracy: 0.9413 - 1s/epoch - 26ms/step

Epoch 17/100

51/51 - 1s - loss: 0.1109 - Accuracy: 0.9525 - val_loss: 0.1544 - val_Accuracy: 0.9413 - 1s/epoch - 26ms/step

Epoch 18/100

51/51 - 1s - loss: 0.1133 - Accuracy: 0.9500 - val_loss: 0.1417 - val_Accuracy: 0.9426 - 1s/epoch - 26ms/step

Epoch 19/100

51/51 - 1s - loss: 0.1129 - Accuracy: 0.9519 - val_loss: 0.1372 - val_Accuracy: 0.9426 - 1s/epoch - 25ms/step

Epoch 20/100

51/51 - 1s - loss: 0.1117 - Accuracy: 0.9507 - val_loss: 0.1274 - val_Accuracy: 0.9426 - 1s/epoch - 26ms/step

Epoch 21/100

51/51 - 1s - loss: 0.1073 - Accuracy: 0.9572 - val_loss: 0.1299 - val_Accuracy: 0.9426 - 1s/epoch - 26ms/step

Epoch 22/100

51/51 - 1s - loss: 0.1132 - Accuracy: 0.9510 - val_loss: 0.1376 - val_Accuracy: 0.9438 - 1s/epoch - 26ms/step

Epoch 23/100

51/51 - 1s - loss: 0.1104 - Accuracy: 0.9532 - val_loss: 0.1203 - val_Accuracy: 0.9438 - 1s/epoch - 26ms/step

Epoch 24/100

51/51 - 1s - loss: 0.1062 - Accuracy: 0.9538 - val_loss: 0.1377 - val_Accuracy: 0.9413 - 1s/epoch - 26ms/step

Epoch 25/100

51/51 - 1s - loss: 0.1056 - Accuracy: 0.9538 - val_loss: 0.1269 - val_Accuracy: 0.9438 - 1s/epoch - 25ms/step

Epoch 26/100

51/51 - 1s - loss: 0.1077 - Accuracy: 0.9544 - val_loss: 0.1380 - val_Accuracy: 0.9426 - 1s/epoch - 25ms/step

Epoch 27/100

51/51 - 1s - loss: 0.1074 - Accuracy: 0.9532 - val_loss: 0.1152 - val_Accuracy: 0.9538 - 1s/epoch - 26ms/step

Epoch 28/100

51/51 - 1s - loss: 0.1049 - Accuracy: 0.9560 - val_loss: 0.1238 - val_Accuracy: 0.9488 - 1s/epoch - 27ms/step

Epoch 29/100

51/51 - 1s - loss: 0.1057 - Accuracy: 0.9525 - val_loss: 0.1159 - val_Accuracy: 0.9526 - 1s/epoch - 26ms/step

Epoch 30/100

51/51 - 1s - loss: 0.1084 - Accuracy: 0.9516 - val_loss: 0.1257 - val_Accuracy: 0.9488 - 1s/epoch - 26ms/step

Epoch 31/100

51/51 - 1s - loss: 0.1079 - Accuracy: 0.9538 - val_loss: 0.1125 - val_Accuracy: 0.9551 - 1s/epoch - 25ms/step

Epoch 32/100

51/51 - 1s - loss: 0.1067 - Accuracy: 0.9544 - val_loss: 0.1060 - val_Accuracy: 0.9538 - 1s/epoch - 27ms/step

Epoch 33/100

51/51 - 1s - loss: 0.1077 - Accuracy: 0.9569 - val_loss: 0.1097 - val_Accuracy: 0.9538 - 1s/epoch - 26ms/step

Epoch 34/100

51/51 - 1s - loss: 0.1036 - Accuracy: 0.9557 - val_loss: 0.1098 - val_Accuracy: 0.9538 - 1s/epoch - 26ms/step

Epoch 35/100

51/51 - 1s - loss: 0.1086 - Accuracy: 0.9572 - val_loss: 0.1164 - val_Accuracy: 0.9538 - 1s/epoch - 26ms/step

Epoch 36/100

51/51 - 1s - loss: 0.1038 - Accuracy: 0.9535 - val_loss: 0.1117 - val_Accuracy: 0.9576 - 1s/epoch - 26ms/step

Epoch 37/100

51/51 - 1s - loss: 0.1014 - Accuracy: 0.9591 - val_loss: 0.1049 - val_Accuracy: 0.9551 - 1s/epoch - 25ms/step

Epoch 38/100

51/51 - 1s - loss: 0.1007 - Accuracy: 0.9535 - val_loss: 0.1090 - val_Accuracy: 0.9563 - 1s/epoch - 26ms/step

Epoch 39/100

51/51 - 1s - loss: 0.1033 - Accuracy: 0.9579 - val_loss: 0.1126 - val_Accuracy: 0.9551 - 1s/epoch - 26ms/step

Epoch 40/100

51/51 - 1s - loss: 0.0996 - Accuracy: 0.9569 - val_loss: 0.1025 - val_Accuracy: 0.9588 - 1s/epoch - 28ms/step

Epoch 41/100

51/51 - 1s - loss: 0.1000 - Accuracy: 0.9579 - val_loss: 0.1009 - val_Accuracy: 0.9563 - 1s/epoch - 26ms/step

Epoch 42/100

51/51 - 1s - loss: 0.1064 - Accuracy: 0.9525 - val_loss: 0.0961 - val_Accuracy: 0.9625 - 1s/epoch - 26ms/step

Epoch 43/100

51/51 - 1s - loss: 0.1006 - Accuracy: 0.9554 - val_loss: 0.1014 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 44/100

51/51 - 1s - loss: 0.1000 - Accuracy: 0.9572 - val_loss: 0.1027 - val_Accuracy: 0.9576 - 1s/epoch - 27ms/step

Epoch 45/100

51/51 - 1s - loss: 0.1008 - Accuracy: 0.9541 - val_loss: 0.1034 - val_Accuracy: 0.9576 - 1s/epoch - 26ms/step

Epoch 46/100

51/51 - 1s - loss: 0.0976 - Accuracy: 0.9569 - val_loss: 0.1039 - val_Accuracy: 0.9551 - 1s/epoch - 26ms/step

Epoch 47/100

51/51 - 1s - loss: 0.1070 - Accuracy: 0.9522 - val_loss: 0.0952 - val_Accuracy: 0.9613 - 1s/epoch - 25ms/step

Epoch 48/100

51/51 - 1s - loss: 0.1002 - Accuracy: 0.9569 - val_loss: 0.0986 - val_Accuracy: 0.9588 - 1s/epoch - 26ms/step

Epoch 49/100

51/51 - 1s - loss: 0.1002 - Accuracy: 0.9575 - val_loss: 0.1024 - val_Accuracy: 0.9551 - 1s/epoch - 25ms/step

Epoch 50/100

51/51 - 1s - loss: 0.0980 - Accuracy: 0.9554 - val_loss: 0.0974 - val_Accuracy: 0.9613 - 1s/epoch - 27ms/step

Epoch 51/100

51/51 - 1s - loss: 0.0954 - Accuracy: 0.9575 - val_loss: 0.0977 - val_Accuracy: 0.9613 - 1s/epoch - 27ms/step

Epoch 52/100

51/51 - 1s - loss: 0.0941 - Accuracy: 0.9594 - val_loss: 0.0988 - val_Accuracy: 0.9613 - 1s/epoch - 27ms/step

Epoch 53/100

51/51 - 1s - loss: 0.1042 - Accuracy: 0.9554 - val_loss: 0.1000 - val_Accuracy: 0.9613 - 1s/epoch - 27ms/step

Epoch 54/100

51/51 - 1s - loss: 0.1009 - Accuracy: 0.9560 - val_loss: 0.0965 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 55/100

51/51 - 1s - loss: 0.0990 - Accuracy: 0.9575 - val_loss: 0.0967 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 56/100

51/51 - 1s - loss: 0.0967 - Accuracy: 0.9585 - val_loss: 0.0944 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 57/100

51/51 - 1s - loss: 0.0956 - Accuracy: 0.9579 - val_loss: 0.0929 - val_Accuracy: 0.9600 - 1s/epoch - 27ms/step

Epoch 58/100

51/51 - 1s - loss: 0.0973 - Accuracy: 0.9582 - val_loss: 0.0921 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 59/100

51/51 - 1s - loss: 0.0996 - Accuracy: 0.9566 - val_loss: 0.0937 - val_Accuracy: 0.9613 - 1s/epoch - 25ms/step

Epoch 60/100

51/51 - 1s - loss: 0.0958 - Accuracy: 0.9579 - val_loss: 0.0958 - val_Accuracy: 0.9600 - 1s/epoch - 25ms/step

Epoch 61/100

51/51 - 1s - loss: 0.1043 - Accuracy: 0.9557 - val_loss: 0.0912 - val_Accuracy: 0.9613 - 1s/epoch - 27ms/step

Epoch 62/100

51/51 - 1s - loss: 0.0952 - Accuracy: 0.9597 - val_loss: 0.0928 - val_Accuracy: 0.9600 - 1s/epoch - 25ms/step

Epoch 63/100

51/51 - 1s - loss: 0.0964 - Accuracy: 0.9569 - val_loss: 0.0932 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 64/100

51/51 - 1s - loss: 0.0920 - Accuracy: 0.9607 - val_loss: 0.0921 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 65/100

51/51 - 1s - loss: 0.0947 - Accuracy: 0.9566 - val_loss: 0.0923 - val_Accuracy: 0.9613 - 1s/epoch - 25ms/step

Epoch 66/100

51/51 - 1s - loss: 0.0935 - Accuracy: 0.9588 - val_loss: 0.0924 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 67/100

51/51 - 1s - loss: 0.0950 - Accuracy: 0.9597 - val_loss: 0.0920 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 68/100

51/51 - 1s - loss: 0.0933 - Accuracy: 0.9554 - val_loss: 0.0922 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 69/100

51/51 - 1s - loss: 0.0940 - Accuracy: 0.9554 - val_loss: 0.0944 - val_Accuracy: 0.9600 - 1s/epoch - 25ms/step

Epoch 70/100

51/51 - 1s - loss: 0.0981 - Accuracy: 0.9566 - val_loss: 0.0888 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 71/100

51/51 - 1s - loss: 0.0918 - Accuracy: 0.9607 - val_loss: 0.0911 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 72/100

51/51 - 1s - loss: 0.0935 - Accuracy: 0.9563 - val_loss: 0.0920 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 73/100

51/51 - 1s - loss: 0.0966 - Accuracy: 0.9560 - val_loss: 0.0923 - val_Accuracy: 0.9588 - 1s/epoch - 26ms/step

Epoch 74/100

51/51 - 1s - loss: 0.0930 - Accuracy: 0.9575 - val_loss: 0.0905 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 75/100

51/51 - 1s - loss: 0.0930 - Accuracy: 0.9600 - val_loss: 0.0906 - val_Accuracy: 0.9600 - 1s/epoch - 26ms/step

Epoch 76/100

51/51 - 1s - loss: 0.0968 - Accuracy: 0.9566 - val_loss: 0.0961 - val_Accuracy: 0.9613 - 1s/epoch - 25ms/step

Epoch 77/100

51/51 - 1s - loss: 0.0888 - Accuracy: 0.9591 - val_loss: 0.0932 - val_Accuracy: 0.9625 - 1s/epoch - 25ms/step

Epoch 78/100

51/51 - 1s - loss: 0.0929 - Accuracy: 0.9597 - val_loss: 0.0900 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 79/100

51/51 - 1s - loss: 0.0916 - Accuracy: 0.9607 - val_loss: 0.0899 - val_Accuracy: 0.9576 - 1s/epoch - 25ms/step

Epoch 80/100

51/51 - 1s - loss: 0.0920 - Accuracy: 0.9613 - val_loss: 0.0920 - val_Accuracy: 0.9588 - 1s/epoch - 25ms/step

Epoch 81/100

51/51 - 1s - loss: 0.0922 - Accuracy: 0.9588 - val_loss: 0.0900 - val_Accuracy: 0.9613 - 1s/epoch - 26ms/step

Epoch 82/100

51/51 - 1s - loss: 0.0972 - Accuracy: 0.9560 - val_loss: 0.0888 - val_Accuracy: 0.9613 - 1s/epoch - 25ms/step

----
train shape: (3203, 600, 1)

score on val: 0.961298406124115

score on train: 0.9644083380699158
----
training time (s): 113.8620

Plot training and evaluate the model#

We can plot the training and validation accuracy and loss to visualize the training progress.

acc = history.history['Accuracy']
val_acc = history.history['val_Accuracy']
epochs = range(1, len(acc) + 1)

fig, axs = plt.subplots(1, 2, figsize=(8, 4))
axs[0].plot(epochs, acc, c='#12B5CB', label='Training')
axs[0].plot(epochs, val_acc, c='#425066', label='Validation')
axs[0].set_title('Training and validation accuracy\n')
axs[0].set_xlabel('Epochs')
axs[0].set_ylabel('Accuracy')
axs[0].legend()

loss = history.history['loss']
val_loss = history.history['val_loss']

axs[1].plot(epochs, loss, c='#12B5CB', label='Training')
axs[1].plot(epochs, val_loss, c='#425066', label='Validation')
axs[1].set_title('Training and validation loss\n')
axs[1].set_xlabel('Epochs')
axs[1].set_ylabel('Loss')
axs[1].legend()
plt.tight_layout()
plt.show()

best_epoch = val_acc.index(max(val_acc)) + 1
print(f'Best epoch: {best_epoch} (accuracy={max(val_acc):.4f})')

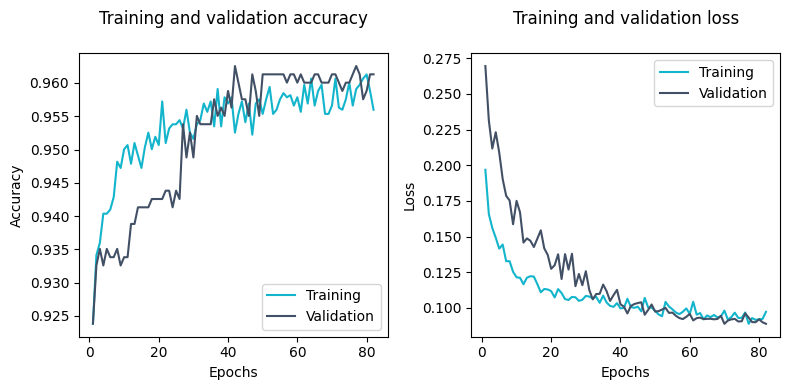
../_images/942b6f1ac1f153d3077252e4ed48c4657368f9eeef00d1ede63a9207bef2a40f.png

Best epoch: 42 (accuracy=0.9625)

We can plot the ROC curve and the confusion matrix to further evaluate our trained model.

y_preds = new_model.predict(x_test, verbose=0).ravel()
fpr, tpr, thresholds = roc_curve(y_test, y_preds)

fig, axs = plt.subplots(1, 2, figsize=(8, 4))
axs[0].plot([0, 1], [0, 1], 'y--')
axs[0].plot(fpr, tpr, marker='.')
axs[0].set_xlabel('False positive rate')
axs[0].set_ylabel('True positive rate')
axs[0].set_title('ROC curve\n')

optimal_threshold = thresholds[np.argmax(tpr - fpr)]
y_pred2 = (new_model.predict(x_test, verbose=0) >= optimal_threshold).astype(int)
cm = confusion_matrix(y_test, y_pred2)
disp = ConfusionMatrixDisplay(confusion_matrix=cm)
disp.plot(cmap='Blues', ax=axs[1])
axs[1].set_title('Confusion matrix\n')
plt.tight_layout()
plt.show()

print(f'Area under curve, AUC = {auc(fpr, tpr)}')
print(f'Optimal threshold value = {optimal_threshold}')

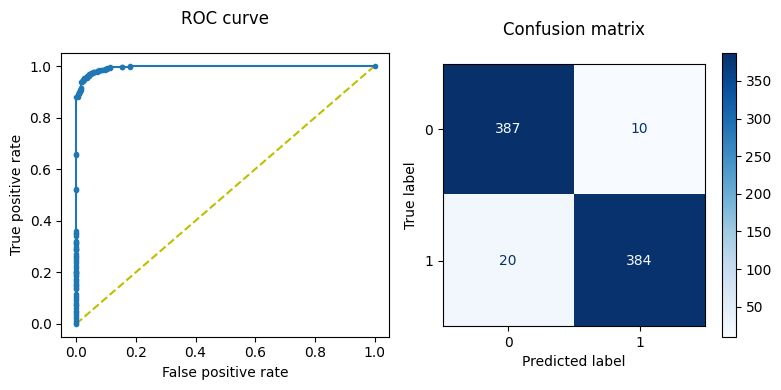
../_images/bd1c04165a79b1c212a78983fd6e08bc93e7067889c227fbcedffc529d305db0.png

Area under curve, AUC = 0.9953612489712447
Optimal threshold value = 0.648914635181427

Save trained model and training settings#

Finally, we save the trained model to an .h5 file and the training settings to a text file.

new_model.save('../results/lstm_transfer.h5')

with open('../results/tl_training_settings.txt', 'w') as text_file:
    text_file.write('\n'.join(f'{i}: {settings[i]}' for i in settings))

/opt/miniconda3/envs/miniml/lib/python3.9/site-packages/keras/src/engine/training.py:3103: UserWarning: You are saving your model as an HDF5 file via `model.save()`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')`.
  saving_api.save_model(